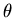 è un insieme finito di associazioni tra variabili e termini, della forma
è un insieme finito di associazioni tra variabili e termini, della forma
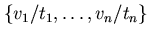 , con le variabili
, con le variabili
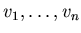 distinte tra di loro e
distinte tra di loro e
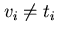 per i=1,
per i=1,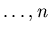 .
.
In questa sezione sarà trattato il meccanismo che permette di calcolare legami tra variabili e valori, obbiettivo principale dei sistemi di programmazione logica.
Una sostituzione 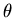 è un insieme finito di associazioni tra variabili e termini, della forma
è un insieme finito di associazioni tra variabili e termini, della forma
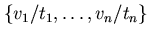 , con le variabili
, con le variabili
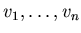 distinte tra di loro e
distinte tra di loro e
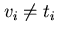 per i=1,
per i=1,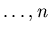 .
.
Un termine è ground se non contiene variabili.
Una sostituzione è detta ground quando ogni termine 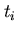 è ground .
è ground .
Una espressione è un termine, oppure un letterale oppure
una congiunzione o disgiunzione di letterali. Sia E una espressione e
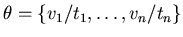 una sostituzione.L'espressione
una sostituzione.L'espressione 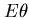 , detta istanza di E secondo
, detta istanza di E secondo 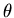 , è il risultato dell'applicazione di
, è il risultato dell'applicazione di 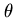 ad E, ottenuto rimpiazzando simultaneamente ogni occorrenza di variabile
ad E, ottenuto rimpiazzando simultaneamente ogni occorrenza di variabile 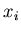 in E con il termine
in E con il termine 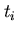 per
per 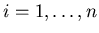 .
.
Se E è ground, allora E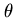 è chiamata istanza ground di E.
Una sostituzione
è chiamata istanza ground di E.
Una sostituzione 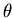 è più generale di una sostituzione
è più generale di una sostituzione 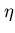 se esiste una sostituzione
se esiste una sostituzione  per cui
per cui
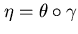 .
.
Dato un programa P, con ground(P) indichiamo l'insieme di tutte le istanze ground delle clausole in P.
Dati le espressioni 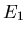 ed
ed 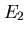 una sostituzione
una sostituzione 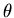 è un unificatore per tali espressioni se
è un unificatore per tali espressioni se
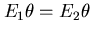 . Un unificatore
. Un unificatore 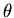 per
per 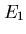 ed
ed 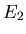 è detto most general unifier (mgu) se, per ogni unificatore
è detto most general unifier (mgu) se, per ogni unificatore  per
per  ed
ed  , esiste una sostituzione
, esiste una sostituzione 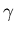 tale che
tale che
 .
.
A Robinson è dovuto il seguente teorema:
Esiste un algoritmo (algoritmo di unificazione) che, prese due espressioni qualsiasi, produce il corrispondente mgu se sono unificabili. Altrimenti termina notificando la non esistenza di tale unificatore.