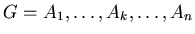 un goal e
un goal e
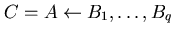 una clausola del programma P. Se
una clausola del programma P. Se 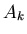 è l'atomo selezionato secondo la regola di selezione ed esiste
è l'atomo selezionato secondo la regola di selezione ed esiste 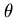 mgu di
mgu di 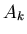 ed A, il goal G' =
ed A, il goal G' =
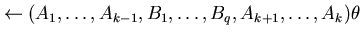 è detto risolvente di G e C.
è detto risolvente di G e C.
La semantica dei programmi logici può essere data seguendo due approcci equivalenti, quello dichiarativo, che vedremmo brevemente nelle sezione successiva, e quello procedurale che si basa sul metodo di risoluzione SLD.
Sia
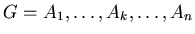 un goal e
un goal e
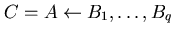 una clausola del programma P. Se
una clausola del programma P. Se 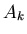 è l'atomo selezionato secondo la regola di selezione ed esiste
è l'atomo selezionato secondo la regola di selezione ed esiste 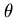 mgu di
mgu di 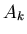 ed A, il goal G' =
ed A, il goal G' =
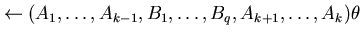 è detto risolvente di G e C.
è detto risolvente di G e C.
Una derivazione SLD di P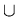 {G} consiste di una sequenza (finita o infinita)
{G} consiste di una sequenza (finita o infinita) 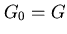 ,
, 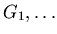 di goal, una sequenza di
di goal, una sequenza di
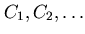 di varianti di clausole di P e una sequenza
di varianti di clausole di P e una sequenza
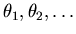 di mgu tale che ogni
di mgu tale che ogni 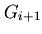 è derivato da
è derivato da 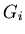 e
e 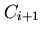 usando
usando 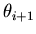 .
.
È indispensabile che ogni 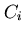 non contenga variabili già apparse nella derivazione fino a
non contenga variabili già apparse nella derivazione fino a 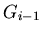 : quindi è necessaria una fase di ridenominazione delle variabili.
: quindi è necessaria una fase di ridenominazione delle variabili.
Una refutazione SLD di P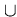 {G} è una derivazione SLD di P
{G} è una derivazione SLD di P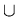 {G} che ha la clausola vuota
{G} che ha la clausola vuota  come ultimo risolvente.
come ultimo risolvente.
Una derivazione SLD è detta fallita se è finita e non è una refutazione.
Una sostituzione di risposta calcolata per 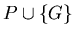 è una sostituzione ottenuta restringendo la composizione
è una sostituzione ottenuta restringendo la composizione
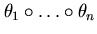 alle variabili di G, dove
alle variabili di G, dove
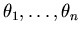 e la sequenza di mgu usati in una refutazione SLD di P
e la sequenza di mgu usati in una refutazione SLD di P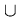 {G}.
{G}.
Una regola di computazione è una funzione da un insieme di goal a un insieme di atomi che, dato un goal, restituisce un atomo di tale goal detto atomo selezionato.
Una derivazione (risp. refutazione) SLD via R è una derivazione (risp refutazione) SLD nella quale per selezionare gli atomi è sempre usata la regola R.
TEOREMA di indipendenza dalla regola di computazione
Se esiste una refutazione SLD di 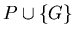 con risposta calcolata
con risposta calcolata 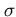 , allora per ogni regola di computazione R esiste una refutazione SLD di
, allora per ogni regola di computazione R esiste una refutazione SLD di 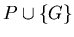 via R con risposta calcolata
via R con risposta calcolata 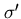 tale che
tale che 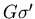 è una variante di
è una variante di 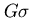 .
.
Sia P un programma e G un goal. Un albero SLD per 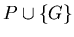 è un albero che soddisfa le seguenti condizioni:
è un albero che soddisfa le seguenti condizioni:
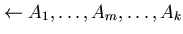 un nodo dell'albero e
un nodo dell'albero e 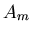 sia l'atomo selezionato. Allora, per ogni clausola di input
sia l'atomo selezionato. Allora, per ogni clausola di input
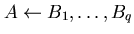 tale che
tale che  e A sono unificabili con mgu
e A sono unificabili con mgu 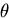 , il nodo ha un figlio
, il nodo ha un figlio 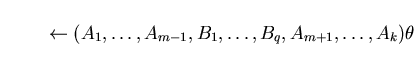
Ogni ramo di un albero SLD è una derivazione di 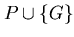 . Rami corrispondenti a derivazioni infinite sono detti rami infiniti.
. Rami corrispondenti a derivazioni infinite sono detti rami infiniti.
I sistemi PROLOG standard utilizzano la regola di computazione che seleziona sempre l'atomo più a sinistra (leftmost) insieme ad una regola di ricerca depth-first.