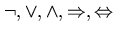 .
.
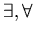 .
.
Una teoria del primo ordine è costituita da un alfabeto, da un linguaggio del primo ordine, da un insieme di assiomi e da un insieme di regole di inferenza. Il linguaggio del primo ordine è costituito da formule ben formate della teoria. Gli assiomi sono un sottoinsieme delle formule ben formate. Gli assiomi e le regole di inferenza permettono di derivare teoremi sulla base della teoria.
Un alfabeto è dato dalle seguenti classi di simboli:
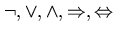 .
.
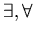 .
.
Un linguaggio del primo ordine su un dato alfabeto è un insieme di formule costruite a partire dai simboli di quell'alfabeto.
Nel seguito, indicheremo i linguaggi del primo ordine con la coppia 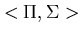 , dove
, dove 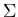 è una segnatura e
è una segnatura e 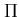 è un insieme di simboli di predicato.
è un insieme di simboli di predicato.
Per definire le formule ben formate definiamo un termine induttivamente:
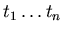 allora f
allora f
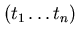 è un termine.
è un termine.
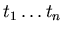 sono termini, allora p
sono termini, allora p
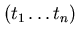 è una formula (atomo).
è una formula (atomo).
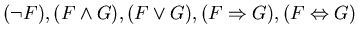 sono formule.
sono formule.
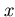 è una variabile, allora
è una variabile, allora
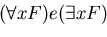 sono formule.
sono formule.
Un letterale è un atomo o la negazione di un atomo.
Una clausola è una formula del tipo
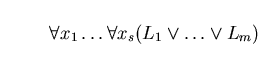
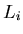 è un letterale e
è un letterale e
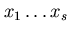 sono tutte le variabili occorrenti in
sono tutte le variabili occorrenti in
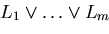 .
.
Poichè in programmazione logica si manipolano clausole, adotteremo una notazione speciale detta forma clausale. Quindi denoteremo la clausola
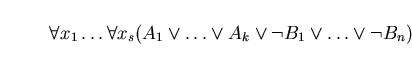
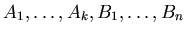 sono atomi e
sono atomi e
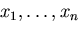 sono tutte le variabili occorrenti in tali atomi, per mezzo di
sono tutte le variabili occorrenti in tali atomi, per mezzo di
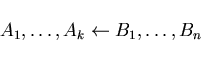
Una clausola di programma è una clausola del tipo
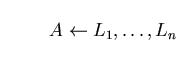
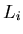 sono letterali positivi, la clausola è detta generale, altrimenti è detta clausola di Horn.
sono letterali positivi, la clausola è detta generale, altrimenti è detta clausola di Horn.
A è detta testa della clausola, mentre
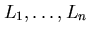 costituiscono il corpo.
costituiscono il corpo.
Una clausola del tipo 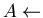 è detta unitaria, o fatto.
è detta unitaria, o fatto.
Un goal è una clausola della forma
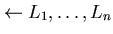 , dove ogni
, dove ogni 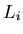 è detto sottogoal. Il simbolo
è detto sottogoal. Il simbolo  denota la clausola vuota, cioè una clausola con corpo e testa vuoti e viene interpretato come una contraddizione.
denota la clausola vuota, cioè una clausola con corpo e testa vuoti e viene interpretato come una contraddizione.
Un programma logico è un insieme finito non vuoto di clausole di programma. Se almeno una delle clausole è generale, il programma sarà detto generale.
Una level mapping di un programma generale è una funzione dall'insieme di simboli di predicato agli interi non negativi. Il valore della level mapping rispetto ad un simbolo di predicato è detto livello di quel simbolo di predicato.
Un programma generale è stratificato se ha una level mapping tale che, in ogni clausola di programma
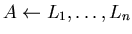 il livello del simbolo di predicato di ogni letterale positivo (risp. negativo) nel corpo è minore o uguale (risp. minore) al livello del simbolo di predicato in A.
il livello del simbolo di predicato di ogni letterale positivo (risp. negativo) nel corpo è minore o uguale (risp. minore) al livello del simbolo di predicato in A.
Le seguenti definizioni di due classi di programmi logici saranno utili nei capitoli successivi, in particolar modo riguardo alla negazione intensionale.
Un programma logico è detto n.v.i.(not variable introducing) se per ogni sua clausola del tipo
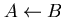 vale che nel corpo B occorrono solo variabili che occorrono nella testa A.
vale che nel corpo B occorrono solo variabili che occorrono nella testa A.
Un programma logico è detto left linear se ogni testa delle sue clausole non contiene occorrenze multiple della stessa variabile.