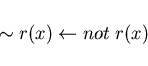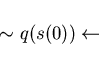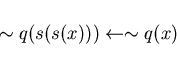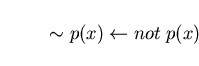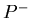
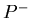
Questo modulo ottiene il programma  complemento di P semplicemente facendo l'unione di comp(P1) e comp(P2).
complemento di P semplicemente facendo l'unione di comp(P1) e comp(P2).
Un esempio riassuntivo può essere:
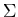 dell'esempio 6.5, con i modi
dell'esempio 6.5, con i modi 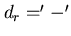 ,
,  ,
, 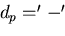 ,
,
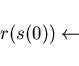
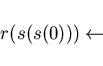
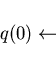
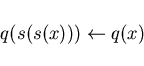
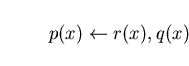
l'analizzatore stabilirà che P1={r,p}, mentre P2={q}.
Infatti il criterio dovrà essere applicato alle queries
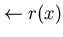 ,
,
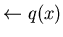 e
e
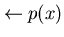 .
.
Nel caso di
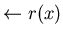 , si avrà che, poiché le clausole la cui testa unifica con
, si avrà che, poiché le clausole la cui testa unifica con  sono tutte fatti e quindi terminanti, il predicato
sono tutte fatti e quindi terminanti, il predicato 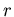 è inserito in P1.
Le risposte ottenute sono
è inserito in P1.
Le risposte ottenute sono
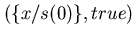 e
e
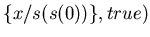 .
.
Successivamente si passa ad esaminare
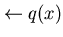 :
la clausola
:
la clausola
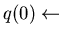 è terminante, mentre per la clausola ricorsiva
è terminante, mentre per la clausola ricorsiva
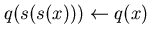 bisogna verificare le due condizioni sugli argomenti.
In questo caso, fallisce subito la prima, cioè quella che impone che le norme dei termini non ground di input siano limitate:
infatti
bisogna verificare le due condizioni sugli argomenti.
In questo caso, fallisce subito la prima, cioè quella che impone che le norme dei termini non ground di input siano limitate:
infatti
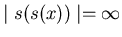 perché
perché 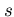 è un costruttore riflessivo in
è un costruttore riflessivo in 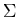 .
.
Esaminando infine
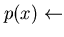 , si ha che la clausola
, si ha che la clausola
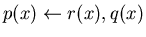 è terminante perché la query
è terminante perché la query
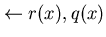 termina.
Infatti
termina.
Infatti
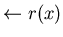 termina con risposte
termina con risposte
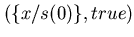 e
e
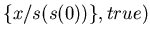 e terminano le query ottenute da
e terminano le query ottenute da
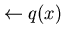 applicandovi tali risposte.
applicandovi tali risposte.
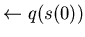 termina perché non unifica con alcuna clausola, mentre
termina perché non unifica con alcuna clausola, mentre
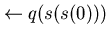 termina perché la clausola con cui unifica è terminante, valendo sulle norme la condizione imposta dal criterio (
termina perché la clausola con cui unifica è terminante, valendo sulle norme la condizione imposta dal criterio (
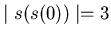

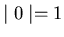 ).
).
Quindi comp(P) = comp(P1)  comp(P2) sarà:
comp(P2) sarà: