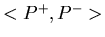6.2.3 Interprete

La procedura di risoluzione che permette, dato un programma P rappresentato come la coppia 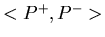$< P^{+} , P^{-}>$, di calcolare risposte a goal che contengono anche letterali negativi non ground segue il metodo descritto da Chan.

Poichè i programmi considerati sono n.v.i., la procedura di normalizzazione delle risposte risulta inutile. Tale procedura ha lo scopo di eliminare dalle risposte le variabili, le eguaglianze e le diseguaglianze ridondanti, intese come quelle che non contengono variabili presenti nel goal. Nella nostra situazione, tali casi sono evitati in partenza perchè il processo di risoluzione non coinvolgerà variabili che non siano già contenute nel goal.

In una prima fase tutte le occorrenze di letterali negativi del tipo 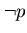$\neg p$ nel goal vengono sostituite da occorrenze del corrispondente predicato 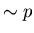$\sim p$ definito in 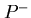$P^{-}$, che viene trattato come un qualunque altro predicato.

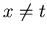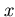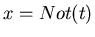Quando la derivazione ottenuta termina in una clausola che contiene solo diseguaglianze primitive (es. $x\neq t$), si potrà, utilizzando l'informazione disponibile sul tipo di $x$, risolvere tale diseguaglianza in una disgiunzione di eguaglianze, sfruttando l'operatore Not di complementazione di un termine definito nell'ambito della negazione intensionale (risulterà $x=Not(t)$).