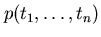 , definiamo
, definiamo
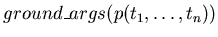 = {
= {
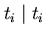 è ground }.
Inoltre, definiamo
è ground }.
Inoltre, definiamo
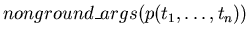 =
=
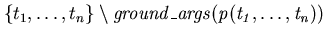
L'analizzatore partizionerà l'insieme dei predicati del programma in base a condizioni sufficienti per la terminazione. Infatti, a causa della nota indecidibilità dell' halting problem, le tecniche effettive di decisione sulla terminazione dei programmi possono verificare solamente criteri sufficienti ma non necessari.
È auspicabile, per l'efficienza del metodo di negazione, che le tecnica usata identifichi una classe di programmi terminanti che approssimi il meglio possibile la classe dei programmi che effettivamente terminano.
Qui di seguito esporremo un criterio che verifica condizioni sufficienti per la terminazione di programmi normali stratificati nvi, left linear, i cui predicati non siano mutuamente ricorsivi (tale ultima ipotesi non è affatto restrittiva perchè con tecniche di unfolding ogni programma mutuamente ricorsivo può essere trasformato in un altro equivalente non mutuamente ricorsivo).
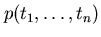 , definiamo
, definiamo
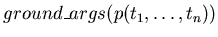 = {
= {
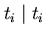 è ground }.
Inoltre, definiamo
è ground }.
Inoltre, definiamo
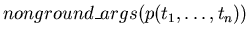 =
=
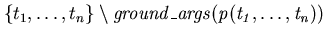
Dato un atomo
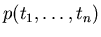 e un modo
e un modo 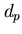 , definiamo
, definiamo
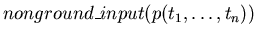 = {
= {
 }.
}.
Il criterio stabilisce se una query del tipo
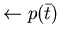 termina rispetto ad un modo
termina rispetto ad un modo 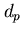 .
Per i nostri scopi, sarà necessario applicarlo a ogni query del tipo
.
Per i nostri scopi, sarà necessario applicarlo a ogni query del tipo
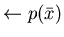 ,
, 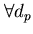 ,
,
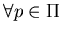 .
In questo modo si otterrà la partizione di
.
In questo modo si otterrà la partizione di 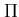 desiderata, in base alle proprietà di terminazione dei predicati in
desiderata, in base alle proprietà di terminazione dei predicati in 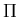 per goal totalmente non ground.
per goal totalmente non ground.
Il criterio testa la terminazione di una particolare query e non di un generico predicato essenzialmente per utilizzare le informazioni che si ottengono durante l'applicazione del criterio stesso.
Infatti, poiché la verifica di terminazione di una query richiederà in generale (cioè quando non si ha a che fare con clausole unitarie) l'applicazione ricorsiva del criterio, tale applicazione potrà essere più mirata nel senso di utilizzare le informazioni sugli argomenti della query, che saranno contenute nella sostituzione 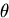 iniziale.
iniziale.
Dato il programma
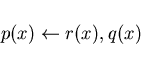
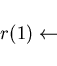
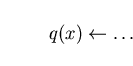
l'applicazione del criterio alla query
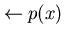 renderà sufficiente, una volta stabilito che la query
renderà sufficiente, una volta stabilito che la query
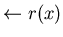 termina per x=1, verificare la terminazione della query
termina per x=1, verificare la terminazione della query
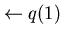 .
.
Il criterio consiste essenzialmente in una applicazione accorta della risoluzione SLDCNF, nel senso che si procede al passo successivo di risoluzione solo quando sono verificate condizioni sufficienti alla terminazione. In effetti i casi critici sono quelli di clausole ricorsive: in tal caso deve essere verificata una particolare condizione sulle norme degli argomenti del predicato che ricorre.
Una query del tipo
 termina, rispetto al modo
termina, rispetto al modo 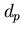 , con risposte
, con risposte
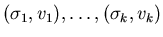 , dove
, dove 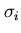 è una sostituzione e
è una sostituzione e 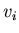 è un insieme di vincoli (diseguaglianze soddisfacibili o primitive), nel caso in cui:
è un insieme di vincoli (diseguaglianze soddisfacibili o primitive), nel caso in cui:
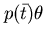 sia un letterale positivo, se ogni clausola la cui testa unifica con
sia un letterale positivo, se ogni clausola la cui testa unifica con
 è terminante con risposte
è terminante con risposte
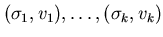 .
.
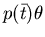 sia un letterale negativo della forma
sia un letterale negativo della forma 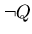 , se la query
, se la query 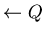 termina, rispetto a
termina, rispetto a 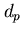 , con risposte
, con risposte
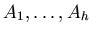 e
e
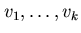 sono la negazione di
sono la negazione di
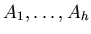 e
e
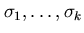 sono uguali a
sono uguali a 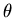 .
.
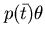 sia una uguaglianza del tipo
sia una uguaglianza del tipo 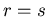 , se
, se
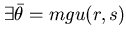 e
e
 e
e 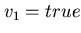 (k=1).
(k=1).
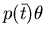 sia una disuguaglianza, se è valida, con risposta
sia una disuguaglianza, se è valida, con risposta
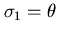 e
e  , altrimenti se è insoddisfacibile, senza risposta (k=0).
, altrimenti se è insoddisfacibile, senza risposta (k=0).
Una query del tipo
 termina senza risposta se
termina senza risposta se
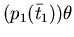 è una diseguaglianza insoddisfacibile, altrimenti termina con risposte
è una diseguaglianza insoddisfacibile, altrimenti termina con risposte
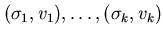 se
se
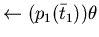 termina con risposta
termina con risposta
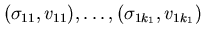 e
e
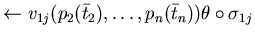 ,
,
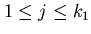 , terminano con risposte
, terminano con risposte
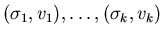 .
.
Una clausola che unifica con
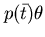 se è della forma :
se è della forma :
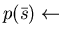 , è terminante con risposta
, è terminante con risposta
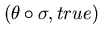 , dove
, dove
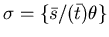 .
.
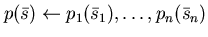 e
e 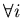
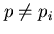 (cioè non è ricorsiva) è terminante con risposta
(cioè non è ricorsiva) è terminante con risposta
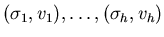 se la query
se la query
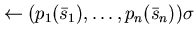 , dove
, dove
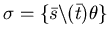 , termina con risposta
, termina con risposta
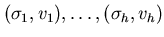 , con i modi calcolati secondo il teorema 6.1.
, con i modi calcolati secondo il teorema 6.1.
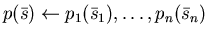 è terminante con risposte
è terminante con risposte
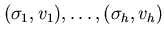 se, posto
se, posto
![$i = min \{j \in [1,n] \mid p_{j} = p \}$](img977.png) e i modi sono calcolati secondo il teorema 6.1, valgono le seguenti condizioni:
e i modi sono calcolati secondo il teorema 6.1, valgono le seguenti condizioni:
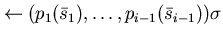 , dove
, dove
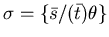 termina con risposte
termina con risposte
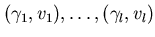 .
.
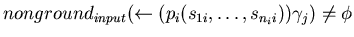 ,
,
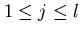 , allora le norme di tali termini devono essere limitate e
, allora le norme di tali termini devono essere limitate e
![$\forall k \in [1,\ldots ,n]$](img983.png)
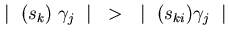 altrimenti deve valere,
altrimenti deve valere,
![$\forall k\in [1,\ldots ,n]$](img985.png) ,
,
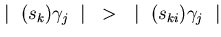 . Siano
. Siano
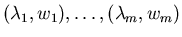 le risposte alle query
le risposte alle query
 ,
,
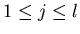 .
.
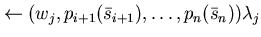 ,
,
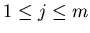 , terminano con risposte
, terminano con risposte
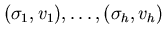 .
.
Dato un programma P e la query
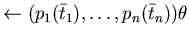 , il criterio applicato a tale query termina.
, il criterio applicato a tale query termina.
dim. (per induzione sulla lunghezza della query)
Il criterio applicato a
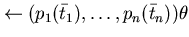 termina perché
termina perché
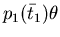 è una disuguaglianza insoddisfacibile oppure perché termina applicato alle queries
è una disuguaglianza insoddisfacibile oppure perché termina applicato alle queries
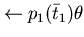 e
e
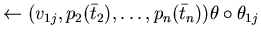 .
.
Quindi è sufficiente dimostrare che il criterio termina se viene applicato alla query del tipo
 .
.
In questo caso termina:
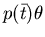 è una uguaglianza
è una uguaglianza
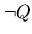 : infatti, poiché il programma P si assume sia stratificato, procedendo per induzione sul valore di level mapping dei predicati, si può fare la seguente ipotesi induttiva:
le queries del tipo
: infatti, poiché il programma P si assume sia stratificato, procedendo per induzione sul valore di level mapping dei predicati, si può fare la seguente ipotesi induttiva:
le queries del tipo
 , con valore di level mapping di
, con valore di level mapping di 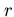 minore di quello di Q, terminano.
Allora anche
minore di quello di Q, terminano.
Allora anche 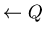 termina, perché può dar luogo solo ad applicazioni del criterio a query il cui valore di level mapping é minore.
termina, perché può dar luogo solo ad applicazioni del criterio a query il cui valore di level mapping é minore.
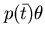 è un letterale positivo e il criterio applicato ad ogni clausola la cui testa unifica con
è un letterale positivo e il criterio applicato ad ogni clausola la cui testa unifica con
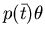 stabilisce se tale clausola è terminante o meno.
stabilisce se tale clausola è terminante o meno.
Infatti se:
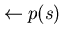 , con
, con 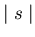
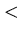
 , termini. Allora si possono avere due casi:
che almeno una clausola la cui testa unifica con
, termini. Allora si possono avere due casi:
che almeno una clausola la cui testa unifica con 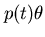 sia non terminante (cioè non vale la condizione sulle norme), nel qual caso il criterio termina, oppure tutte siano terminanti:
in questo caso la clausola
sia non terminante (cioè non vale la condizione sulle norme), nel qual caso il criterio termina, oppure tutte siano terminanti:
in questo caso la clausola
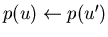 risolve con
risolve con 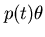 con mgu
con mgu 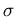 ottenendo la query
ottenendo la query
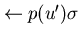 .
Poiché vale la condizione sulle norme si può applicare l'ipotesi induttiva e quindi il criterio termina.
Infine, il criterio applicato alla query
.
Poiché vale la condizione sulle norme si può applicare l'ipotesi induttiva e quindi il criterio termina.
Infine, il criterio applicato alla query
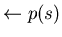 , con
, con 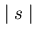 = 1, termina perchè tale query può unificare solo con clausole ricorsive non terminanti o con clausole non ricorsive terminanti.
= 1, termina perchè tale query può unificare solo con clausole ricorsive non terminanti o con clausole non ricorsive terminanti.

Dato un programma P, la query
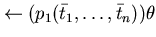 termina con risposte
termina con risposte
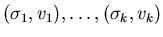
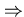 tale query ha un albero di derivazione SLDCNF finito con sostituzioni di risposta
tale query ha un albero di derivazione SLDCNF finito con sostituzioni di risposta
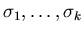 e diseguaglianze primitive
e diseguaglianze primitive
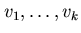 .
.
dim. (per induzione sulla struttura del programma e della query)
Consideriamo il caso in cui la query sia del tipo
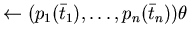 , con
, con 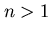 .
.
Se valgono le condizioni del criterio, si può avere che:
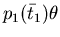 è una diseguaglianza insoddisfacibile e quindi l'albero di radice
è una diseguaglianza insoddisfacibile e quindi l'albero di radice
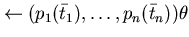 è finito (termina con fail).
è finito (termina con fail).
 non è una diseguaglianza insoddisfacibile e se termina la query corrispondente con risposta
non è una diseguaglianza insoddisfacibile e se termina la query corrispondente con risposta
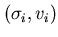
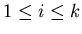 , e le queries
, e le queries
 terminano, l'albero sarà
terminano, l'albero sarà
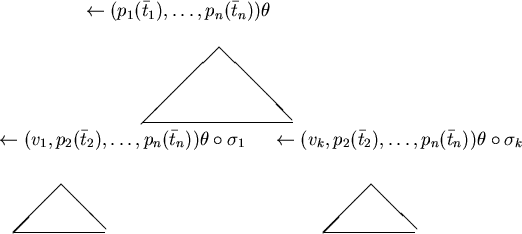
cioè finito.
Dimostriamo ora che una query del tipo
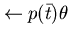 termina, se valgono le condizioni del criterio;
termina, se valgono le condizioni del criterio;
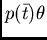 è una diseguaglianza valida, l'albero sarà:
è una diseguaglianza valida, l'albero sarà:
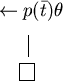
e la risposta è
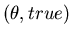 .
.
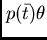 è una diseguaglianza insoddisfacibile, l'albero sarà:
è una diseguaglianza insoddisfacibile, l'albero sarà:
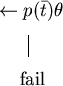
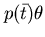 è una uguaglianza del tipo
è una uguaglianza del tipo 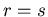 ed esiste
ed esiste 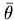 mgu di
mgu di 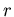 ed
ed 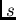 , l'albero sarà:
, l'albero sarà:

con risposta
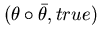 .
.
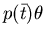 è un letterale negativo della forma
è un letterale negativo della forma 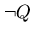 , e la query
, e la query 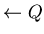 termina con sostituzioni di risposta
termina con sostituzioni di risposta
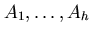 e
e
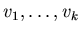 sono la negazione di
sono la negazione di
 , l'albero sarà:
, l'albero sarà:
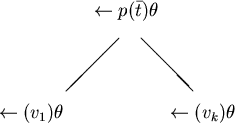
e quindi le risposte saranno
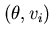 ,
,
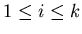 .
.
 è un letterale positivo, procediamo
per induzione sugli strati del programma, supponendo che le queries del tipo
è un letterale positivo, procediamo
per induzione sugli strati del programma, supponendo che le queries del tipo 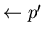 con valore di level mapping di
con valore di level mapping di 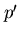 minore di quello di
minore di quello di 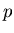 abbiano un albero finito. Dimostriamo che se ogni clausola la cui testa unifica con
abbiano un albero finito. Dimostriamo che se ogni clausola la cui testa unifica con
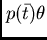 è terminante, l'albero è finito.
è terminante, l'albero è finito.
Si ha che:
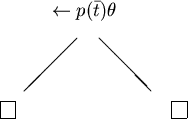
con risposte
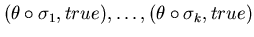 .
.
 non ricorsiva, se valgono le condizioni del criterio, cioè la query
non ricorsiva, se valgono le condizioni del criterio, cioè la query
 termina, l'albero sarà finito perché per ipotesi induttiva tale query ha un albero finito.
termina, l'albero sarà finito perché per ipotesi induttiva tale query ha un albero finito.
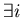 per cui vale
per cui vale 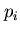
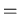
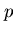 (cioè la clausola è ricorsiva), bisogna dimostrare la correttezza del criterio in riferimento alla chiamata ricorsiva.
(cioè la clausola è ricorsiva), bisogna dimostrare la correttezza del criterio in riferimento alla chiamata ricorsiva.
Procediamo per induzione sul valore della norma considerando separatamente il caso in cui vale
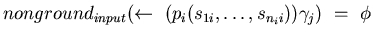 da quello in cui non vale.
Per semplicità, consideriamo il caso di predicati con un solo argomento.
da quello in cui non vale.
Per semplicità, consideriamo il caso di predicati con un solo argomento.
Nel primo caso se vale
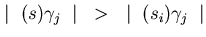 , con
, con
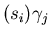 ground, si ha:
ground, si ha:
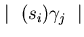 = 1, il termine
= 1, il termine
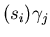 può essere solo o una costante o un termine del tipo
può essere solo o una costante o un termine del tipo  , con g non riflessivo, per come è definita la norma. Quindi il sottogoal
, con g non riflessivo, per come è definita la norma. Quindi il sottogoal
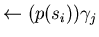 può risolvere solo con clausole che non sono ricorsive, sulle quali il criterio è corretto.
Infatti non esistono clausole ricorsive del tipo
può risolvere solo con clausole che non sono ricorsive, sulle quali il criterio è corretto.
Infatti non esistono clausole ricorsive del tipo
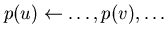 con
con 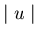 = 1 tale che
= 1 tale che 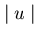
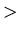
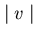 .
.
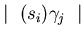 = h, il criterio sia corretto. Allora dimostriamo che vale nel caso che
= h, il criterio sia corretto. Allora dimostriamo che vale nel caso che
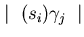 = h+w.
Infatti, se
= h+w.
Infatti, se
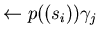 risolve con la clausola
risolve con la clausola
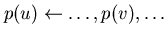 con
con 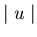 = h+w
= h+w 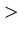
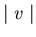 = h e sostituzione
= h e sostituzione 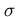 , si ottiene il sottogoal
, si ottiene il sottogoal
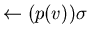 , per cui vale l'ipotesi induttiva.
, per cui vale l'ipotesi induttiva.
Nel secondo caso è utile la seguente osservazione:
se
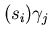 è non ground e vale
è non ground e vale
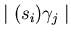
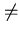
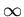 , allora
, allora
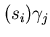 non è una variabile. Infatti se così fosse, non potrebbe valere la relazione
non è una variabile. Infatti se così fosse, non potrebbe valere la relazione
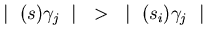 , perché
, perché 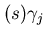 dovrebbe contenere un costruttore riflessivo, eventualità che contraddirebbe l'ipotesi che
dovrebbe contenere un costruttore riflessivo, eventualità che contraddirebbe l'ipotesi che
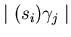
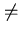
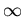 .
.
Quindi, 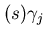 può esser solo del tipo
può esser solo del tipo
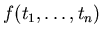 , con
, con
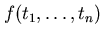
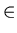
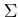 e
e 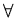 i tale che
i tale che
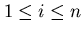 e
e 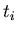 è non ground
è non ground 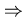
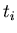
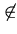
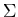 (altrimenti
(altrimenti
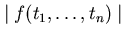 =
= 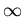 ).
).
Quindi le variabili che compaiono in
 non influiscono sul valore della norma e perciò si può procedere come nel caso precedente, per induzione sul valore della norma.
non influiscono sul valore della norma e perciò si può procedere come nel caso precedente, per induzione sul valore della norma.

La verifica della relazione sulle norme per tutti gli argomenti di una chiamata ricorsiva potrebbe sembrare una condizione troppo forte e si potrebbe pensare di limitarla solo alle posizioni di input. Il seguente esempio fa vedere che tale condizione è necessaria per mantenere la correttezza del criterio:
Considerando la definizione dei numeri pari data dalle clausole
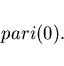
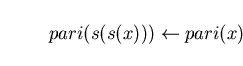
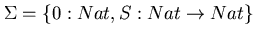 ,
se l'utente volesse usarla per generare tutti i numeri pari fornirebbe il modo
,
se l'utente volesse usarla per generare tutti i numeri pari fornirebbe il modo
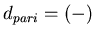 .
Se il criterio controllasse la relazione sulle norme solo per le posizioni di input, stabilirebbe che la query
.
Se il criterio controllasse la relazione sulle norme solo per le posizioni di input, stabilirebbe che la query
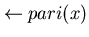 termina, errando. D'altra parte il predicato
termina, errando. D'altra parte il predicato  va trattato con la negazione intensionale.
va trattato con la negazione intensionale.