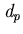 dall'insieme dei naturali {1,..., n} all'insieme {+,-}.
dall'insieme dei naturali {1,..., n} all'insieme {+,-}.
Per rendere possibile l'analisi a tempo di compilazione è necessario avere informazioni sugli argomenti dei predicati. Basandosi su informazioni sul tipo dei termini presenti nelle clausole ricorsive, e sui loro modi, cioè sulla possibilità di avere posizioni occupate da termini ground o meno, il criterio può imporre una relazione che, se non verificata, assicura che la clausola non è terminante.
Quindi di seguito vengono riportate le definizione di modo e della norma utilizzata dal criterio.
Riferendoci a [Plü90] diamo la seguente
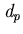 dall'insieme dei naturali {1,..., n} all'insieme {+,-}.
dall'insieme dei naturali {1,..., n} all'insieme {+,-}.
Se
 = '+' chiamiamo i posizione di input di p, intendendo che tali posizioni al momento della chiamata del predicato dovrebbero essere rimpiazzate da termini ground.
Similmente, se
= '+' chiamiamo i posizione di input di p, intendendo che tali posizioni al momento della chiamata del predicato dovrebbero essere rimpiazzate da termini ground.
Similmente, se
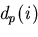 = '-' chiamiamo i posizione di output di p e tale posizione andrà rimpiazzata da un termine non ground.
= '-' chiamiamo i posizione di output di p e tale posizione andrà rimpiazzata da un termine non ground.
Un modo per un programma P è una funzione che assegna ad ogni simbolo di relazione di P un insieme non vuoto di modi.
Per la classe di programmi considerati (n.v.i) è possibile, data una clausola e dato il modo dell'atomo di testa, inferire i modi di ogni letterale di tale clausola, secondo il seguente teorema la cui dimostrazione è immediata.
Data la clausola
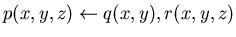 e
e
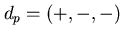 , il teorema permette di inferire per
, il teorema permette di inferire per 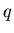 il modo
il modo 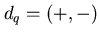 e per
e per 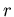
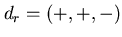 .
.
L'altra nozione fondamentale per la successiva definizione della norma è quella di tipo dei termini:
dato un programma P sul linguaggio L = 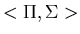 , consideriamo
, consideriamo 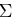 non come una segnatura piatta, ma come una segnatura con una molteplicità di sorte che forniscono informazione di tipo sulla struttura dei termini.
non come una segnatura piatta, ma come una segnatura con una molteplicità di sorte che forniscono informazione di tipo sulla struttura dei termini.
Ogni tipo denotato da una segnatura può essere rappresentato come un grafo. Importante per la definizione di norma sui termini di un certo tipo è la nozione di costruttore riflessivo:
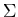 e c costruttore appartenente a
e c costruttore appartenente a 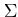 , c è riflessivo se compare in un ciclo del grafo di
, c è riflessivo se compare in un ciclo del grafo di 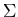 .
. dell'esempio 6.3.
dell'esempio 6.3.
La seguente definizione introduce la norma utilizzata nel criterio proposto; tale definizione permette di distinguere alcuni casi critici per la terminazione.
In particolare, la norma assume il valore convenzionale 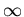 sui termini variabili di una segnatura che contiene costruttori riflessivi.
Questo valore porta il criterio a concludere, insieme ad altre condizioni, che il goal in cui compaiono tali termini può non terminare: infatti la presenza di costruttori riflessivi nella segnatura può portare alla costruzione di termini di lunghezza non finita, causando la non terminazione del programma.
sui termini variabili di una segnatura che contiene costruttori riflessivi.
Questo valore porta il criterio a concludere, insieme ad altre condizioni, che il goal in cui compaiono tali termini può non terminare: infatti la presenza di costruttori riflessivi nella segnatura può portare alla costruzione di termini di lunghezza non finita, causando la non terminazione del programma.
Un esempio di tale problema è il goal
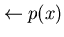 valutato rispetto alla definizione dei numeri pari dell'esempio 3.6.
valutato rispetto alla definizione dei numeri pari dell'esempio 3.6.
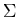 e un tipo
e un tipo 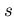 in
in 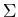 , una norma sui termini di
, una norma sui termini di 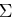 è una funzione così definita:
è una funzione così definita:

dove 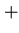 è l'operatore di somma su
è l'operatore di somma su
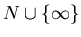 definito nel modo usuale sui naturali e tale che, se
definito nel modo usuale sui naturali e tale che, se 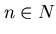 ,
,
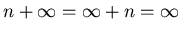 e
e
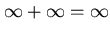 .
.
Se
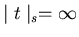 , diciamo che il termine
, diciamo che il termine 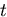 ha norma non limitata.
ha norma non limitata.
Questa norma, ricorrendo solo nel caso di termini costruiti a partire da costruttori riflessivi, è abbastanza generale da fornire valutazioni realistiche in molti casi.
Considerando per esempio la segnatura
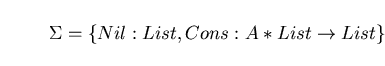
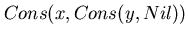 risulta uguale a 3 anche se il termine non è ground.
risulta uguale a 3 anche se il termine non è ground.