7.6 Modularità

I vantaggi, nel campo della ingegneria del software, di un sistema modulare sono ben conosciuti e sono sfruttati dal Gödel. Il sistema modulare del Gödel è basato sull'idea standard che si possono scrivere programmi estesi componendo vari moduli evitando problemi di clash dei nomi e potendo nascondere i dettagli implementativi in particolari moduli di più basso livello.

Essendo la semantica del Gödel migliore, non si hanno i problemi di origine semantica dei vari sistemi modulari del Prolog.

Un programma Gödel è una collezione di moduli; un modulo consiste in generale di due parti: la parte locale e quella export. Nella prima compaiono le dichiarazioni per i simboli utilizzabili solo in questa parte locale, le dichiarazioni dei moduli da cui importare simboli da utilizzare, le dichiarazioni di controllo e le definizioni delle proposizioni e dei predicati che hanno le dichiarazioni in questo modulo.

La parte export consiste delle dichiarazioni di linguaggio e di controllo e delle definizioni di proposizioni e di predicati disponibili nella parte locale e in tutti i moduli che importano tale modulo.

Esempio 7.1  

Un esempio di modulo Gödel è il seguente:

LOCAL 		 M. 


PREDICATE 		 R : T1 $\ast$ T2. 


Member(x,[x 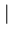$\mid$ xs]). 


Member(x,[z 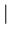$\mid$ xs]) $\leftarrow$ Member(x,xs). 

(x,y) $\leftarrow$ 


IF SOME[z] R(x,z) 


THEN (ALL[x] Member(x,[A,B]) 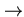$\rightarrow$ P) 


ELSE  P. 

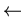$\leftarrow$ Pred(x,y). 


R(x,A). 




EXPORT 		 M. 


IMPORT 		 M1,M2. 


BASE 		 T1,T2. 


CONSTRUCTOR 		 List/1. 


CONSTANT 		 Nil: List(alpha); 


A,B: T2. 


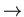FUNCTION 		 Cons : alpha $\ast$ List(alpha) $\rightarrow$ List(alpha);  


F : T1 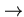$\rightarrow$ T2.  


PREDICATE 		 Member : alpha $\ast$ List(alpha);  


Pred : T1 $\ast$ T2.  


PROPOSITION 		 P.

La gerarchia che è possibile introdurre nel progetto di programmi grazie ai moduli permette di dare una soluzione accettabile ad un problema dovuto ai predicati di Input/Output. Tali predicati non hanno una semantica dichiarativa compromettendo il fine principale del Gödel. È consigliato quindi confinare l'uso di questi predicati in moduli del livello più alto della gerarchia permettendo così di mantenere una semantica dichiarativa chiara per tutti i moduli sottostanti.