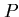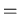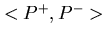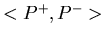 .
È così possibile usare, per valutare i goal, l'ordinaria risoluzione SLD, rimpiazzando tutte le occorrenze di letterali negativi del tipo
.
È così possibile usare, per valutare i goal, l'ordinaria risoluzione SLD, rimpiazzando tutte le occorrenze di letterali negativi del tipo 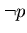 con
con 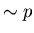 , predicato, definito in
, predicato, definito in 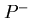 , che rappresenta il complementare di
, che rappresenta il complementare di 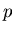 .
.
Un insieme di operatori di base su programmi logici non può non comprendere un operatore di negazione:
nel capitolo precedente è stata presentata una sua definizione per mezzo della negazione intensionale, che permette di ottenere, dato un programma P, una coppia di programmi definiti 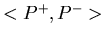 .
È così possibile usare, per valutare i goal, l'ordinaria risoluzione SLD, rimpiazzando tutte le occorrenze di letterali negativi del tipo
.
È così possibile usare, per valutare i goal, l'ordinaria risoluzione SLD, rimpiazzando tutte le occorrenze di letterali negativi del tipo 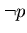 con
con 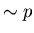 , predicato, definito in
, predicato, definito in 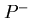 , che rappresenta il complementare di
, che rappresenta il complementare di 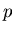 .
.
Ciò porta però ad un eccessivo numero di clausole nel complementare, soprattutto quando il dominio su cui è definito contiene un elevato numero di costanti; la definizione dell'operatore di negazione proposta in questa tesi mira a eliminare questo problema rimandando al tempo di esecuzione, con la risoluzione SLDCNF, il calcolo del complementare per una parte dei predicati presenti nel programma.
La parte negativa 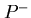 è quindi composta da due tipi di clausole, quelle risultato del processo di negazione con la NI applicato ad una parte dei predicati, e quelle del tipo
è quindi composta da due tipi di clausole, quelle risultato del processo di negazione con la NI applicato ad una parte dei predicati, e quelle del tipo
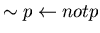 , con
, con 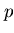 tra i restanti predicati.
tra i restanti predicati.
La partizione dell'insieme dei predicati avviene in base ad un criterio che controlla proprietà sufficienti alla terminazione di goal del tipo
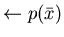 : se il criterio stabilisce che il goal può non terminare, le clausole che definiscono
: se il criterio stabilisce che il goal può non terminare, le clausole che definiscono 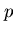 vengono trattate con la NI, altrimenti viene inserita in
vengono trattate con la NI, altrimenti viene inserita in 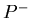 una clausola del tipo visto prima.
una clausola del tipo visto prima.
In questo modo si ovvia al problema evidenziato per la NI e, nel contempo, si utilizza la NC di Chan solo nei casi per cui è dimostrata corretta e completa, quelli per cui l'albero di derivazione risulta finito.
Il criterio proposto si basa sull'uso di una norma sui termini; la segnatura su cui è definito il programma è costituita da una molteplicità di sorte per mezzo delle quali si hanno informazioni di tipo sui termini che compaiono nelle clausole. Queste informazioni vengono sfruttate dalla norma, definita in modo tale da ricorrere solo sui costruttori riflessivi; tra i valori delle norme dei termini che compaiono in clausole ricorsive deve poi valere, affinchè siano giudicate terminanti dal criterio, una particolare relazione. Sono infatti le clausole ricorsive quelle più critiche perchè possono dare origine a computazioni infinite. La relazione sulle norme permette di stabilire, prima di applicare ricorsivamente il criterio al corpo delle clausole, che non si può incorrere in tali casi critici.
Il criterio permette di analizzare programmi generali n.v.i., left linear, condizioni poi necessarie per l'applicazione della NI, e che devono essere anche stratificati: questa condizione è necessaria per assicurare la terminazione del criterio stesso in relazione alla presenza di letterali negativi nel corpo delle clausole.
Nel capitolo, dopo aver presentato in modo più dettagliato le motivazioni che portano a integrare la NI e la NC, viene definita la norma utilizzata nel criterio, e il criterio stesso, di cui viene dimostrata la terminazione e la correttezza.
In seguito viene definita la trasformazione che permette di ottenere la coppia di programmi 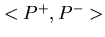 , e ne viene data una dimostrazione informale di correttezza e completezza.
, e ne viene data una dimostrazione informale di correttezza e completezza.
Viene inoltre dimostrato un teorema che permette di ottenere la negazione di una coppia di programmi semplicemente attraverso una opportuna ridenominazione dei predicati.
Infine vengono formulate alcune considerazioni su aspetti legati alla implementazione del metodo proposto.