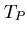
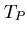
Sia L un linguaggio del primo ordine il cui insieme di costanti è non vuoto. L'universo di Herbrand 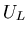 per L è l'insieme di tutti i termini ground di L. La base di Herbrand
per L è l'insieme di tutti i termini ground di L. La base di Herbrand 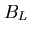 per L è invece definita come l'insieme di tutti gli atomi ground di L.
Una interpretazione di Herbrand per L è un'interpretazione tale che:
per L è invece definita come l'insieme di tutti gli atomi ground di L.
Una interpretazione di Herbrand per L è un'interpretazione tale che:
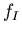 da
da 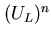 ad
ad 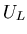 definita assegnando il termine ground
definita assegnando il termine ground
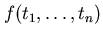 alla sequenza
alla sequenza
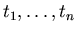 di termini ground.
di termini ground.
Un modello di Herbrand per un insieme di formule S è un'interpretazione di Herbrand per S che sia anche un modello.
Per caratterizzare i modelli di programmi logici, introduciamo l'operatore di conseguenza immediata 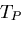 che trasforma interpretazioni di Herbrand in interpretazioni di Herbrand.
Dato un programma P ed un'interpretazione I, poniamo
che trasforma interpretazioni di Herbrand in interpretazioni di Herbrand.
Dato un programma P ed un'interpretazione I, poniamo
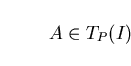
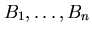 tali che
tali che
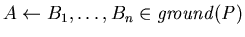 e
e
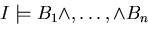
Alternativamente, per un atomo ground A
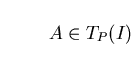
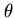 ed una clausola
ed una clausola
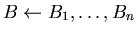 tali che
tali che
 e
e
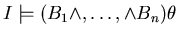 .
.
Elenchiamo ora alcuni risultati fondamentali.
TEOREMA (correttezza della derivazione SLD)
Sia P un programma e
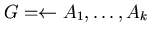 un goal. Supponiamo che esista una refutazione SLD di
un goal. Supponiamo che esista una refutazione SLD di 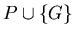 con sequenza di sostituzioni
con sequenza di sostituzioni
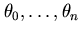 . Allora
. Allora
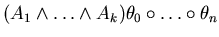 è una conseguenza semantica di P.
è una conseguenza semantica di P.
COROLLARIO
Se esiste una refutazione SLD di 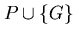 allora
allora 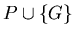 è inconsistente.
è inconsistente.
LEMMA
Sia S un insieme di universali. Se S ha un modello allora ha un modello di Herbrand.
TEOREMA (di Caratterizzazione)
Sia P un programma. Allora P ha un modello di Herbrand 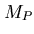 che soddisfa le seguenti proprietà:
che soddisfa le seguenti proprietà:
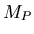 è un modello minimo di P.
è un modello minimo di P.
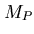 è il minimo fixpoint di
è il minimo fixpoint di 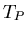 .
.
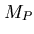 =
=
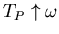 .
.
COROLLARIO
L'insieme di successo di un programma P è contenuto nel suo modello minimo di Herbrand.
Sia P un programma e
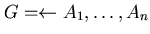 un goal. Diciamo che
un goal. Diciamo che 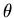 è una sostituzione di risposta corretta per
è una sostituzione di risposta corretta per 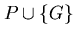 se
se 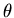 opera solo su variabili presenti in G e vale
opera solo su variabili presenti in G e vale
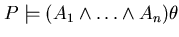 .
.
TEOREMA
Sia P un programma e G un goal. Per ogni sostituzione di risposta corretta  per
per 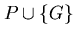 esiste una sostituzione di risposta calcolata
esiste una sostituzione di risposta calcolata 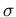 per
per 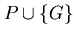 tale che
tale che 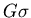 è più generale di
è più generale di 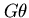 .
.
TEOREMA (Forte Completezza della derivazione SLD)
Dato un programma P ed un goal G, supponiamo che 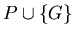 sia inconsistente. Allora ogni albero di derivazione SLD con radice G è di successo.
sia inconsistente. Allora ogni albero di derivazione SLD con radice G è di successo.
TEOREMA (di Successo)
Dato un programma P ed un atomo ground A, i seguenti fatti sono equivalenti:
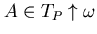 .
.
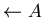 è di successo.
è di successo.
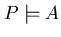 .
.