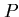
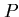
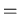
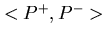
In questa sezione viene esposto un teorema che permette, dato un programma già rappresentato come una coppia, di calcolarne il complementare attraverso una trasformazione sintattica, senza ripercorrere i passi visti.
Dato il programma 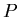 rappresentato come la coppia
rappresentato come la coppia
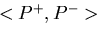
![\begin{displaymath}Not(P) = <P^{-} , P^{+}>_{[p/ \sim p, \sim p / p]_{p \in \Pi}} \end{displaymath}](img1181.png)
dim.
Valendo, secondo [MPRT90], un risultato analogo quando l'operatore 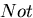 realizza solo la negazione intesionale, è sufficiente dimostrare che la relazione vale sul programma costituito dai predicati, e dalle relative clausole, che il criterio ha stabilito non terminare.
realizza solo la negazione intesionale, è sufficiente dimostrare che la relazione vale sul programma costituito dai predicati, e dalle relative clausole, che il criterio ha stabilito non terminare.
Si considerino quindi le clausole del tipo
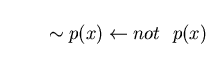
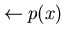 termina e l'unica clausola che definisce
termina e l'unica clausola che definisce 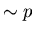 è quella appena vista, anche
è quella appena vista, anche
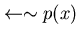 termina.
Quindi applicando la negazione costruttiva e assumendo che
termina.
Quindi applicando la negazione costruttiva e assumendo che 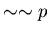
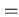
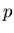 , si ottiene la clausola che definisce
, si ottiene la clausola che definisce 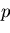 :
: 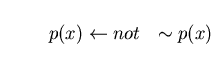
Tale clausola corrisponde a quella ottenuta secondo la trasformazione sintattica.
Poiché il programma finale si ottiene con l'unione dei complementari delle due partizioni, la relazione vale.
