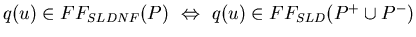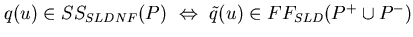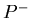 che denoterà il complemento di
che denoterà il complemento di 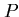 .
.
Utilizzando gli operatori di unione e intersezione visti in precedenza, è possibile dare una definizione dell'operatore di negazione intensionale [MPRT90] per una particolare classe di programmi che estende quella per cui era stata data la definizione precedente.
Tali programmi ammettono l'uso di letterali negativi nel corpo delle clausole; non ammettono invece variabili locali al corpo delle clausole: è importante notare che tale ultimo vincolo non limita l'espressività dei programmi ottenibili rispetto a quelli non n.v.i.
Come nella definizione precedente di NI, si otterrà un nuovo programma 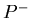 che denoterà il complemento di
che denoterà il complemento di 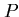 .
.
La classe di programmi considerata è la seguente:
Dato un linguaggio del primo ordine
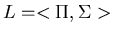 , con il simbolo di predicato binario
, con il simbolo di predicato binario 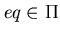 , la classe dei programmi logici su
, la classe dei programmi logici su 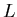 è induttivamente definita come segue:
è induttivamente definita come segue:
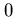 è un programma (il programma vuoto);
è un programma (il programma vuoto);
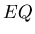 :
: 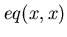 è un programma;
è un programma;
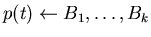 è un programma, dove
è un programma, dove 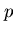 è un simbolo in
è un simbolo in  differente da
differente da 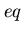 ,
, 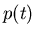 è un atomo non ristretto, e
è un atomo non ristretto, e
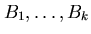 è una congiunzione di letterali in
è una congiunzione di letterali in 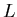 .
.
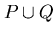 è un programma se
è un programma se 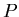 e
e 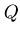 lo sono.
lo sono.
A questo punto è utile introdurre un modo alternativo di definire il complemento di un programma logico, che si basa sull'idea di considerare la negazione come un tipo particolare di informazione positiva.
Si considererà il linguaggio del primo ordine sottostante il programma come esteso a 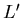 =
=
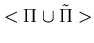 dove
dove 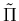 =
=
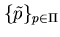 .
I letterali in
.
I letterali in 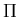 saranno chiamati letterali positivi e quelli in
saranno chiamati letterali positivi e quelli in 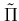 letterali negativi.
letterali negativi.
I programmi definiti le teste delle cui clausole sono positive (rispettivamente negative) vengono detti programmi positivi (rispettivamente negativi).
Sarà inoltre necessario distinguere tra il programma vuoto positivo 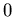 e quello vuoto negativo
e quello vuoto negativo 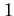 .
.
L'operatore di complementazione, avuto un programma positivo (risp. negativo), restituisce un programma negativo (risp. positivo) che rappresenta la conoscenza complementare implicitamente contenuta nel programma originale.
Il complemento di un programma 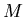 è denotato da
è denotato da 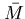 .
.
Per induzione sulla struttura di 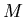 ,
, 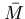 è definito come segue:
è definito come segue:
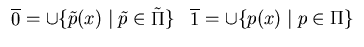
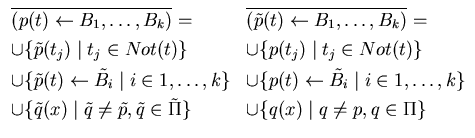
dove 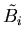 =
=
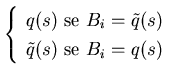
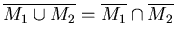
=
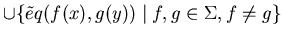
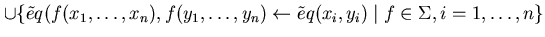
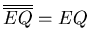
L'idea è quella di trasformare un programma 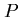 sul linguaggio
sul linguaggio
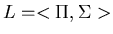 nella coppia di programmi definiti
nella coppia di programmi definiti 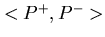 sul linguaggio esteso
sul linguaggio esteso
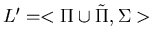 .
.
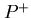 è il programma positivo che rappresenta l'informazione positiva di
è il programma positivo che rappresenta l'informazione positiva di 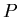 , mentre
, mentre  è il programma negativo che rende esplicita l'informazione negativa di
è il programma negativo che rende esplicita l'informazione negativa di 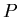 .
Ciò è formalizzato nella seguente definizione:
.
Ciò è formalizzato nella seguente definizione:
Sia 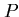 un programma. Allora
un programma. Allora
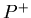 è ottenuto da
è ottenuto da  rimpiazzando ogni letterale negativo
rimpiazzando ogni letterale negativo 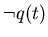 con
con 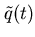 ;
;
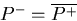
Dato il programma
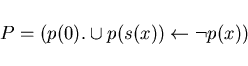
si ottiene
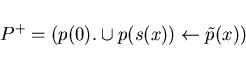
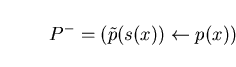
La possibilità di trattare programmi come una coppia di programmi definiti permette di fare a meno della regola di negazione come fallimento finito nel processo di valutazione delle queries su  , rimpiazzandola con l'ordinaria risoluzione SLD su
, rimpiazzandola con l'ordinaria risoluzione SLD su 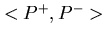 .
La correttezza di questo procedimento è provata dal seguente teorema:
.
La correttezza di questo procedimento è provata dal seguente teorema:
Per ogni atomo ground  in
in  , con
, con  linguaggio del programma
linguaggio del programma 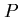 :
:
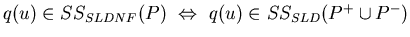
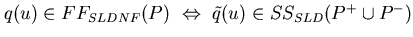
e, dualmente,