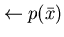 termina secondo il criterio, il complementare del predicato
termina secondo il criterio, il complementare del predicato 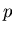 viene calcolato con la negazione di Chan, in caso contrario con la negazione intensionale.
viene calcolato con la negazione di Chan, in caso contrario con la negazione intensionale.
Il metodo per realizzare l'operatore di negazione proposto in questa tesi integra le tecniche di negazione intensionale e di negazione costruttiva di Chan.
L'idea è di determinare, con un'analisi a tempo di compilazione, a quali predicati applicare la negazione intensionale e a quali invece la negazione costruttiva. Questa partizione dei predicati viene decisa con un criterio che controlla condizioni sufficienti per la terminazione di goal totalmente non ground:
in pratica, se il goal
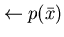 termina secondo il criterio, il complementare del predicato
termina secondo il criterio, il complementare del predicato 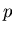 viene calcolato con la negazione di Chan, in caso contrario con la negazione intensionale.
viene calcolato con la negazione di Chan, in caso contrario con la negazione intensionale.
Per fornire le basi per la formulazione del criterio, in questo capitolo vengono presentati alcuni degli approcci presenti in letteratura al problema della terminazione di programmi logici.
L'indecidibilità dell'halting problem per le macchine di Turing stabilisce che non esiste un algoritmo che individui tutti e soli i programmi terminanti. Poiché ogni funzione Turing-calcolabile può essere calcolata da un programma Prolog, è di conseguenza indecidibile il loop-checking per il Prolog.
Quindi uno dei problemi cruciali della programmazione logica (in particolare quella in Prolog) è quello di evitare computazioni infinite, permettendo così lo sviluppo di software affidabile.
L'attenzione è naturalmente incentrata sulla ricorsione visto che è l'unica potenziale fonte di computazioni infinite, dal momento che mancano nella struttura di ogni programma logico costrutti quali while, for ecc. tipici invece di programmi imperativi.
Quando si parla di terminazione di programmi logici, si identificano due vie diverse [VP86]. Nella prima si considera la terminazione esistenziale che afferma che un programma termina se e solo se fallisce finitamente o produce almeno una derivazione di successo. Nella seconda via si considera la terminazione universale che stabilisce che un programma termina se e solo se tutte le sue derivazioni sono finite.
La terminazione esistenziale può essere considerata ragionevole in alcune applicazioni dove l'interesse principale è quello di sapere se esiste una soluzione ad un particolare problema. In generale però questo approccio è limitativo; infatti è importante la validità della seguente affermazione:
dati due goal 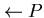 e
e 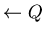 le cui computazioni terminano, allora la computazione del goal
le cui computazioni terminano, allora la computazione del goal
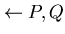 termina.
termina.
Secondo la terminazione esistenziale, questa deduzione non è vera; considerando infatti:
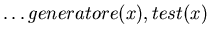 , dove generatore produce un numero infinito di soluzioni e test fallisce per ognuna di esse, si ha che tale goal dà luogo ad una computazione infinita.
, dove generatore produce un numero infinito di soluzioni e test fallisce per ognuna di esse, si ha che tale goal dà luogo ad una computazione infinita.
Di conseguenza per affrontare tale problema in programmazione logica si parla di solito di terminazione universale che fornisce una nozione più forte e che gode inoltre della proprietà di non dipendere dalle regole di selezione delle clausole. Naturalmente anche la terminazione universale, come quella esistenziale, non può non dipendere dalla regola di computazione.
La stesura di programmi di una certa dimensione in linguaggio Prolog è divenuta realtà solo negli ultimi anni e quindi il problema della terminazione di programmi logici sta diventando sempre più uno degli argomenti di maggiore interesse nella ricerca ed è oggetto di molti studi.
Sono numerose le tesi formulate e sono diversi gli approcci seguiti per realizzarle.
Bezem [Bez89] ha analizzato in dettaglio il problema della terminazione forte, ovvero di quali programmi terminano per tutti i goal ground e per tutte le regole di selezione. Ha introdotto la nozione di programma ricorrente dimostrando che è una proprietà necessaria e sufficiente per la terminazione forte.
Un programma P è ricorrente se esiste una level mapping
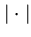 (funzione
(funzione
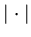
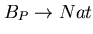 che associa ad ogni atomo ground
che associa ad ogni atomo ground 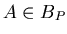 un numero naturale che ne individua la size)
per ogni clausola
un numero naturale che ne individua la size)
per ogni clausola
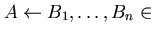 ground(P) tale che
ground(P) tale che
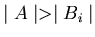 per ogni
per ogni ![$i \in [1,n]$](img582.png) .
.
Inoltre Bezem sfruttando il concetto di boundedness di un goal (un atomo A è bounded rispetto ad una level mapping
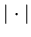 se essa è limitata sull'insieme
se essa è limitata sull'insieme ![$[A]$](img584.png) di tutte le istanze ground di A, un goal è bounded se lo sono tutti i suoi atomi)
ha dimostrato che:
di tutte le istanze ground di A, un goal è bounded se lo sono tutti i suoi atomi)
ha dimostrato che:
dato un programma P ricorrente e G un goal bounded, allora tutte le SLD-derivazioni di 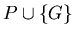 sono finite.
sono finite.
Sebbene molti programmi ricorsivamente definiti sulla struttura dei termini, quali append, member, nqueens e altri, risultino essere ricorrenti, la nozione di ricorrenza è troppo restrittiva; infatti una vasta classe di programmi, tra cui quicksort, mergesort, risulta essere non ricorrente e quindi non terminante fortemente. Questo fatto è dovuto principalmente alla presenza di variabili locali, cioè di risultati intermedi passati alle chiamate ricorsive.
Le prove di terminazione per tali programmi si basano essenzialmente sull'assunzione che tali valori siano calcolati prima che i letterali ricorsivi siano chiamati; tale assunzione è naturalmente giustificata, nel contesto Prolog, dalla sua regola di computazione left-to-right.
Bossi, Cocco e Fabris [BCF91], partendo dall'idea di Bal Wang e Shyamasundar [BS91] degli U-grafi (che registrano le connessioni rilevanti attraverso l'unificazione tra il programma e gli atomi del goal) e sfruttando level-mapping applicate ad atomi non ground, hanno dimostrato la terminazione dei cicli dei grafi per una classe di termini che godono della proprietà di rigidità. I termini rigidi possono avere variabili, ma la size di tali termini non è modificata dalle sostituzioni. Un esempio tipico è la listsize che mappa le liste nel numero che uguaglia la loro lunghezza e i termini che non sono liste sono mappati alla costante 0. La lunghezza di una lista è indipendente dalla istanziazione dei suoi elementi. D'altra parte la terminazione di programmi quali append ecc. non dipende dal fatto che le liste date inizialmente abbiano elementi ground. Questa situazione si presenta tipicamente per tipi di dato polimorfi.
Apt e Pedreschi [AP90,AP91], estendendo i risultati di Bezem, hanno caratterizzato i programmi left-terminanti per queries ground (e bounded) con la regola di computazione Prolog. Hanno introdotto la nozione di accettabilità (estensione di quella di ricorrenza), sviluppando un metodo di prova basato sull'equivalenza di programmi accettabili e left-terminanti.
Un programma P è detto left-terminante se tutte le LD-derivazioni di P che iniziano con un goal ground sono finite (poichè si considera il metodo di risoluzione SLD con la sola regola del Prolog e S in SLD sta per selection rule, LD-risoluzione denota Linear Resolution for Definite Clauses).
Sia P un programma,
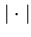 una norma per P ed I un modello (non necessariamente di Herbrand) per P.
P è detto accettabile rispetto alla norma
una norma per P ed I un modello (non necessariamente di Herbrand) per P.
P è detto accettabile rispetto alla norma
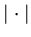 ed al modello I se per ogni clausola
ed al modello I se per ogni clausola
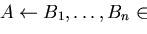 ground(P) vale:
ground(P) vale:
![\begin{displaymath}\mid A \mid > \mid B_{i} \mid \forall i \in [1, \bar{n}] \end{displaymath}](img589.png)
![$\bar{n} = min(\{n\} \cup \{ i \in [1,n] \mid I \not \models B_{i})$](img590.png)
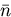 può essere altresì definito:
può essere altresì definito:
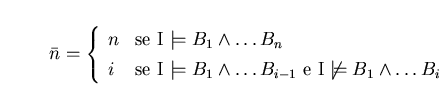
P è accettabile se è accettabile secondo una qualche norma
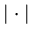 e modello I.
e modello I.
Partendo da queste definizioni Apt e Pedreschi sono arrivati ai seguenti risultati:
Lemma. Ogni programma ricorrente è accettabile.
Teorema. Sia P un programma accettabile e G un goal bounded, allora tutte le LD-derivazioni di 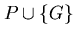 sono finite.
sono finite.
Osservando che ogni goal ground G è bounded si ottiene il seguente
Corollario. Ogni programma accettabile è left terminante.
Gli ultimi risultati stabiliscono la coincidenza tra le nozioni di accettabilità e left terminazione.
Teorema. Sia P un programma left terminante. Allora esistono una norma
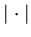 e un modello I per P tali che:
e un modello I per P tali che:
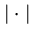 e I;
e I;
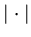 e I se e solo se tutte le LD-derivazioni di
e I se e solo se tutte le LD-derivazioni di 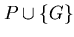 sono finite.
sono finite.
Corollario. Un programma è left terminante se e solo se è accettabile.
Il problema della verifica automatica di terminazione di programmi Prolog costituisce un settore di studi assai attivo. Ricordiamo che qualsiasi metodo automatico di prova fornisce solo condizioni sufficienti per la terminazione.
Ullman e Van Gelden [UvG88] hanno studiato la questione che la valutazione top-down (Prolog-like) di un insieme di regole logiche potesse avere una garanzia di terminazione, trattando così il problema delle variabili locali. Nel loro approccio vengono prima generati degli insiemi di disequazioni tra le sizes degli argomenti dei simboli di relazione (interargument inequalities), successivamente viene verificato se in effetti tali diseguaglianze sono valide.
Plümer [Plü90] introduce la nozione di linear predicate inequalities (una forma più generale di quella di [UvG88]) e descrive una tecnica per la derivazione automatica di disequazioni lineari valide. Un'assunzione fondamentale in questo approccio è che gli argomenti di input dei predicati ricorsivi siano ground ogni volta che tali predicati vengono invocati. Tali informazioni sono fornite da un'analisi data-flow.
In [Plü91] la tecnica per la generazione automatica di prove di terminazione per programmi Prolog viene estesa considerando input rigidi, e perciò possibilmente non ground, usando norme semi-lineari.
Verschaetse e De Schreye [VDS91] hanno presentato una tecnica per provare la terminazione di programmi Prolog a tempo di compilazione.
Si procede essenzialmente trasformando un dato programma in una forma astratta, che esprime la relazione esistente tra le sizes degli argomenti dei predicati occorrenti nel programma originale. Si può inoltre ottenere facilmente un'approssimazione lineare di tali relazioni. La prova di terminazione infine viene effettuata risolvendo sistemi di equazioni lineari.
Si osservi che l'approccio proposto da Apt e Pedreschi rispetto a quello di Ullman e Van Gelder, Plümer, Verschaetse e De Schreye, sono in un certo senso complementari. Gli ultimi hanno come obbiettivo la verifica automatica della terminazione di un programma Prolog puro e di un goal. Un tale approccio non potrà, come già sottolineato, mai aspirare alla completezza, per la nota indecibilità dell'halting problem. Apt e Pedreschi invece propongono un metodo di prova completo che caratterizza precisamente i programmi left terminanti. Però d'altra parte è vero che non si determina alcuna condizione per una possibile automazione del metodo.