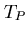L'uso della logica come linguaggio di programmazione è assai recente. Sino agli anni '70 essa era stata solo un indispensabile supporto teorico, nell'ambito della ricerca in Intelligenza Artificiale, sia alla formalizzazione di concetti sia alla definizione di sistemi di deduzione automatica, ma non costituiva un vero modello di calcolo. Solamente in seguito ai risultati di Robinson sul Principio di risoluzione, Kowalski potè dare un'interpretazione procedurale alla Logica in Clausole Horn [vEK76], e contemporaneamente Colmerauer sviluppò il primo linguaggio logico denominato PROLOG, che è ancora oggi il più diffuso.
L'affermazione crescente della programmazione logica è dovuta principalmente alla sua importante proprietà di essere dichiarativa: il programma cioè definisce che cosa si vuol calcolare senza dover specificare come questo deve essere calcolato.
Ciò si traduce nel fatto che nella Logica in Clausole di Horn (HCL) la semantica dichiarativa data in termini di modelli (o tramite l'operatore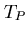 
) è equivalente alla semantica operazionale.
Estensioni della programmazione logica importanti ai fini della progettazione del software sono quelle che permettono di avere una descrizione dei programmi a meta-livello, attraverso sistemi di teorie separate, per orientarsi così verso la programmazione modulare, lo sviluppo incrementale di programmi, l'evolversi dinamico di teorie, forme di ragionamento non monotono, la metaprogrammazione, l'ereditarietà e l'object-orientation.
Per raggiungere questi obbiettivi, in [BMPT90] sono introdotti i metaoperatori oggetto di questa tesi i quali, operando su teorie logiche, permettono di definire un approccio alla costruzione dei programmi sintesi dei due attualmente riconosciuti come più corretti: il primo è l'approccio trasformazionale, nel quale i programmi sono costruiti, a partire da una specifica iniziale, attraverso successive trasformazioni; il secondo quello modulare, nel quale i programmi sono costruiti mettendo insieme moduli preesistenti, visti come scatole nere. Utilizzando gli operatori di unione, intersezione e negazione si combinano questi due approcci dal momento che gli operatori fondono i moduli esistenti per formarne di nuovi, e nel farlo vi applicano delle trasformazioni.
Un altro campo nel quale questi metaoperatori permettono interessanti applicazioni è quello della rappresentazione della conoscenza: per esempio, è possibile, rappresentando porzioni di conoscenza per mezzo di programmi logici, ricostruire in modo formale relazioni gerarchiche grazie a operatori, denominati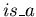 
e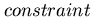 
, definiti a partire da quelli precedentemente citati.
I metaoperatori possono essere anche considerati come le operazioni di base di un metalinguaggio per una versione modulare della programmazione logica: poiché hanno una solida base semantica non presentano i problemi tipici delle primitive extra-logiche assert, retract solitamente offerte dai sistemi Prolog, le quali oltretutto manipolano un singolo modulo.
In questo contesto si inserisce la presente tesi, nella quale dopo aver presentato in modo formale i metaoperatori, viene descritta una loro realizzazione a metalivello utilizzando il linguaggio per la programmazione logica Gödel, e, partendo da questi, viene proposto un metodo per realizzare l'operatore di negazione.
Il problema della negazione nei linguaggi logici è uno degli argomenti di maggiore interesse nel campo della ricerca in programmazione logica, perché la HCL non permette l'uso di alcuna forma di negazione nei programmi. Per questo motivo, nei sistemi Prolog si è introdotta la negazione in forme più o meno limitate, che tuttavia si sono rivelate poco soddisfacenti. La maggior parte di queste realizzazioni si basa sulla regola di negazione come fallimento, proposta originariamente da Clark, che consente di inferire informazione negativa quando il tentativo di dimostrarla in positivo fallisce.
Tale regola pur avendo una giustificazione semantica chiara, ha il difetto di non permettere una simmetria nel trattamento dell'informazione positiva e negativa. Questo si traduce operazionalmente nel fatto che non si possono calcolare valori nelle interrogazioni negative. Tale limitazione risulta assai spiacevole in applicazioni tipiche della programmazione logica, quali basi di dati deduttive e sistemi esperti.
Tra le diverse tecniche proposte per superare questo problema troviamo la negazione intensionale [BaMPT90,Man88] e la negazione costruttiva [Chan88,Chan89]. La prima attraverso un approccio trasformazionale a tempo di compilazione sintetizza il complementare di un programma logico e permette quindi di calcolare risposte a interrogazioni negative, la seconda a tempo di esecuzione costruisce la negazione della risposta alla corrispondente interrogazione positiva e la fornisce come risposta.
La negazione intensionale è stata la tecnica finora usata per realizzare l'operatore di negazione [MPRT90], in quanto, fornendo il complementare del programma, permette di trattare simmetricamente l'informazione positiva e quella negativa definendo la coppia di programmi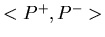 
.
Pur essendo un metodo corretto e completo (sotto particolari ipotesi sulla classe di programmi trattata), la negazione intensionale può essere troppo costosa in alcuni casi. Infatti essa può dar luogo a un numero notevole di nuove clausole che costituiscono il complementare, quando si considerano domini finiti di non piccole dimensioni; tale situazione si presenta per esempio nelle basi di dati deduttive.
D'altra parte la negazione costruttiva è dimostrata essere corretta e completa solamente per alberi di derivazione finiti, in quanto consiste essenzialmente nella completazione delle risposte calcolate per il goal positivo.
Per risolvere questi problemi, in questa tesi viene proposto un metodo per la negazione che integra i due metodi visti. L'obbiettivo è quello di ottenere, nei casi in cui la negazione intensionale dà luogo ad un numero elevato di clausole, un'unica clausola prodotto del processo di complementazione. Attraverso un'analisi del programma eseguita in base alla proprietà di terminazione di una classe di goal, si partiziona l'insieme dei predicati in due sottoinsiemi: quelli che sicuramente terminano per tali goal e quelli che possono non terminare. Per i primi il calcolo effettivo della negazione viene rimandato a tempo di esecuzione, con la negazione costruttiva di Chan, per i secondi si procede con la normale negazione intensionale. Il risultato complessivo viene calcolato applicando l'operatore di unione alle due porzioni ottenute. In questo modo si ottiene, al prezzo di un'analisi del programma a tempo di compilazione, una riduzione del costo in spazio nel calcolo del complementare.
Per effettuare uno studio sulla terminazione adeguato allo scopo, viene proposto un criterio che si basa sull'uso di una particolare norma sui termini e una relazione su tali norme per le clausole ricorsive. Pur non avendo ovviamente pretese di completezza, il criterio proposto, di cui è stata dimostrata la terminazione e la correttezza, si presta bene a individuare i casi critici per l'applicazione della negazione intensionale, casi a cui invece si applica bene la negazione costruttiva di Chan.
Allo studio teorico degli operatori segue la fase di realizzazione, portata a termine utilizzando il linguaggio per la programmazione logica Gödel. Tale linguaggio fornisce una serie di predicati che manipolano la rappresentazione ground di programmi logici, evitando le difficoltà semantiche dei predicati Prolog assert e retract. I programmi oggetto vengono quindi rappresentati come termini del metalivello ottenendo così una semantica più chiara e uno stile di programmazione più pulito.
Sfruttando la struttura modulare che possono avere i programmi Gödel, sono stati realizzati una serie di moduli il principale dei quali, chiamato Shell, mette a disposizione una serie di predicati che manipolano programmi logici oggetto realizzando gli operatori di Unione, Intersezione, Negazione, Is_a e Constraint. Inoltre viene fornito un predicato demo che, data una coppia di programmi risultato dell'applicazione del metodo per la negazione presentato, realizza la risoluzione secondo la negazione costruttiva di Chan. È stato così possibile sperimentare su vari esempi la tecnica di negazione e gli altri operatori.
ORGANIZZAZIONE DELLA TESI
Nel capitolo 2 è presentata la terminologia di base e i concetti principali della teoria della Programmazione Logica.
Nel capitolo 3 sono presentate, dopo l'esposizione delle motivazioni che hanno portato alla negazione come fallimento finito, della sua formulazione e dei suoi limiti, le tecniche della negazione intensionale e della negazione costruttiva di Chan.
Nel capitolo 4 viene fornita una panoramica sulle proposte più significative nell'ambito dello studio della proprietà di terminazione dei programmi logici, fornendo le basi per la formulazione del criterio presentato successivamente.
Nel capitolo 5, dopo aver fornito le definizioni, sia trasformazionale che metainterpretativa, degli operatori unione ed intersezione, ed aver introdotto gli operatori Is_a e Constraint da questi ricavabili, viene riportata la definizione della negazione intensionale per la classe dei programmi logici generali.
Nel capitolo 6, la parte originale di questa tesi insieme al progetto, vengono analizzati i problemi delle tecniche di negazione viste e introdotto un metodo che le integra. Dopo aver presentato lo schema generale della tecnica, si definisce il criterio che verifica proprietà sufficienti alla terminazione, e ne viene dimostrata la terminazione e la correttezza. Vengono inoltre formulate alcune considerazioni sulla negazione della coppia di programmi ottenuta.
Nel capitolo 7 vengono esposti gli aspetti principali del linguaggio utilizzato per la fase di realizzazione.
Nel capitolo 8 sono riportate considerazioni sulla realizzazione del metodo esposto nei capitoli precedenti, e vengono riportati i risultati di alcuni esempi.
Nel capitolo 9 è riportato il listato dei moduli che costituiscono il progetto.