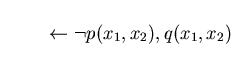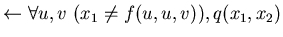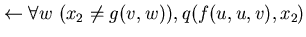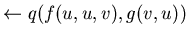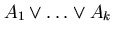 può essere ottenuta negando individualmente ogni
può essere ottenuta negando individualmente ogni 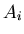
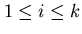 e ricombinando le componenti.
Vedremo che la negazione di ogni
e ricombinando le componenti.
Vedremo che la negazione di ogni 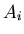 non dà origine a nessun nuovo sottogoal.
non dà origine a nessun nuovo sottogoal.
La negazione di una disgiunzione della forma
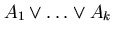 può essere ottenuta negando individualmente ogni
può essere ottenuta negando individualmente ogni 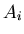
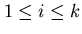 e ricombinando le componenti.
Vedremo che la negazione di ogni
e ricombinando le componenti.
Vedremo che la negazione di ogni 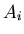 non dà origine a nessun nuovo sottogoal.
non dà origine a nessun nuovo sottogoal.
La procedura ha bisogno di un'accurata trattazione della quantificazione implicita delle variabili quando la negazione della risposte coinvolge variabili.
La procedura è basata sulla seguente equivalenza che è vera per le uguaglianze ma non in generale:
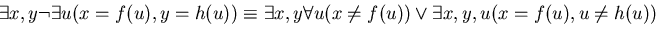
Una risposta normalizzata è della forma
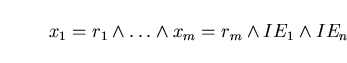
Negando la parte di eguaglianze otteniamo le prime 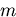 componenti
componenti
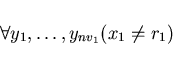
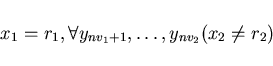
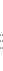
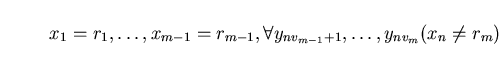
dove
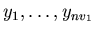 sono non-goal variabili in
sono non-goal variabili in
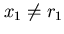 ,
,
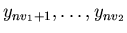 sono non-goal variabili in
sono non-goal variabili in
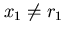 che non sono in
che non sono in
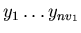 etc.
etc.
Se 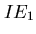 è
è
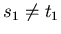 allora la componente seguente è
allora la componente seguente è
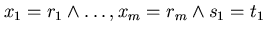 . Lo stesso se
. Lo stesso se 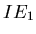 è della forma
è della forma
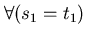 .
Dopo la negazione, le variabili esplicitamente quantificate universalmente vengono implicitamente quantificate esistenzialmente.
.
Dopo la negazione, le variabili esplicitamente quantificate universalmente vengono implicitamente quantificate esistenzialmente.
I componenti successivi sono generati similmente.
Vediamo ora qualche esempio di negazione di risposte.
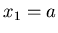 ,
,
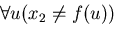 dà la disgiunzione:
dà la disgiunzione:
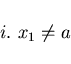
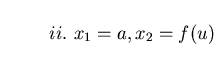
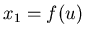 ,
, 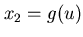 ,
, 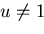 dà la disgiunzione:
dà la disgiunzione:
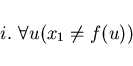
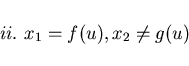
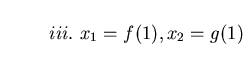
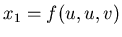 ,
,
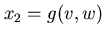 ,
, 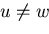 dà la disgiunzione :
dà la disgiunzione :
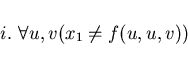
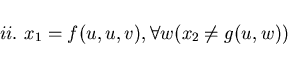
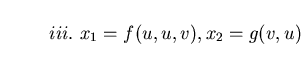
Considerando l'ultima disgiunzione come la negazione delle risposte a
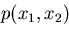 , si ha che il goal
, si ha che il goal