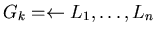 un goal e
un goal e 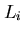 il letterale selezionato.
il letterale selezionato.
Sia
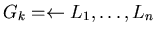 un goal e
un goal e 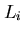 il letterale selezionato.
il letterale selezionato.
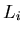 è il predicato di uguaglianza del tipo
è il predicato di uguaglianza del tipo 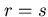 .
Se
.
Se 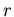 ed
ed 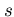 sono unificabili con mgu
sono unificabili con mgu 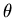 allora il goal derivato è
allora il goal derivato è
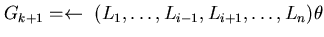 .
.
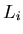 è la disuguaglianza del tipo
è la disuguaglianza del tipo 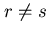 o
o
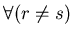 .
Se tale diseguaglianza è valida, allora il goal derivato è
.
Se tale diseguaglianza è valida, allora il goal derivato è
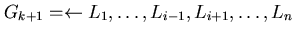 .
.
Se tale diseguaglianza è insoddisfacibile allora il goal 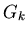 fallisce.
fallisce.
Si noti che le disuguaglianze soddisfacibili ma non valide non sono selezionate.
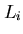 è un letterale positivo.
Se c'è una clausola del programma
è un letterale positivo.
Se c'è una clausola del programma
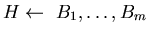 tale che esiste un mgu
tale che esiste un mgu 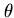 t.c.
t.c.
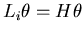 allora il goal derivato è
allora il goal derivato è
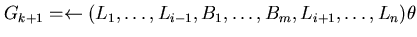 .
.
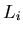 è un letterale negativo della forma
è un letterale negativo della forma
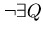 .
.
Si calcolano le risposte a 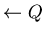 .
.
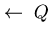 allora
allora
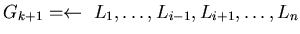 .
.
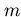 risposte normalizzate
risposte normalizzate
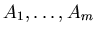 a
a 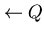 t.c.
t.c.
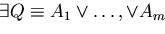 allora
allora 
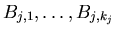 è la
è la 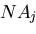 in
in
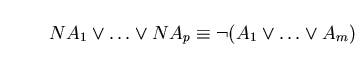
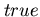 , allora il goal
, allora il goal 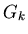 fallisce.
fallisce.
Nelle sezioni successive esporremo il processo di normalizzazione delle risposte a 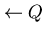 . Vedremo quindi un procedura che permette di ottenere la negazione delle risposte stesse.
. Vedremo quindi un procedura che permette di ottenere la negazione delle risposte stesse.
Una SLDCNF refutazione è una derivazione finita che termina
L'ultimo caso è sempre un caso di terminazione con successo perché le diseguaglianze sono sempre soddisfacibili.