3.1 La negazione come fallimento finito

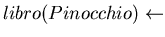
Consideriamo il programma

$libro(Pinocchio) \leftarrow$

$libro(Bibbia) \leftarrow$

$quotidiano(Repubblica) \leftarrow$

$quotidiano(L'unione\_sarda) \leftarrow$

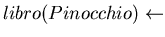
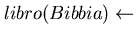
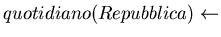
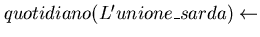
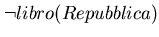la cui interpretazione intuitiva è ovvia. Sembrerebbe ragionevole poter inferire che vale $\neg libro(Repubblica)$, ma ciò non è possibile usando la risoluzione SLD. D'altra parte $\neg libro(Repubblica)$ non è conseguenza logica del programma: infatti esistono modelli in cui 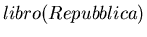$libro(Repubblica)$ è una formula vera.

Tale fatto è generale: consideriamo infatti un programma logico P e un atomo A 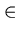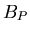$\in$ $B_{P}$ (base di Herbrand associata a P). Si ha che A è conseguenza logica di P se P 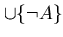$\cup \{ \neg A \}$ è insoddisfacibile. Non possiamo perciò mostrare che 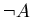$\neg A$ è conseguenza logica di P, dal momento che P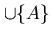$\cup \{A \}$ è sempre soddisfacibile, avendo 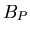$B_{P}$ come modello.

Poiché non è conveniente, per problemi di intrattabilità computazionale, avere a disposizione un theorem prover corretto e completo per la logica del primo ordine, sono necessarie regole speciali per la deduzione di informazione negativa.

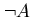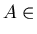
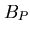Un primo approccio è la Closed World Assumption (CWA), proposta da Reiter [Reiter78], che consente di derivare $\neg A$, con $A \in$ $B_{P}$, ogni volta che da P non è possibile dimostrare (in particolare con la risoluzione SLD) A.

Tale regola di inferenza non è effettiva perché in generale non si può stabilire in tempo finito che un certo atomo segue logicamente da un dato programma.

Quindi si sono cercate regole più deboli della CWA ma effettive. La negazione come fallimento finito (n.a.f.) [Clark78] permette di estendere la risoluzione SLD consentendo di dimostrare la negazione di goal ground quando il goal positivo corrispondente ha un numero finito di derivazioni finite, e tutte falliscono.

Più formalmente definiamo l'insieme di fallimento finito SLD 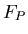$F_{P}$ come l'insieme degli atomi ground A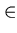 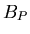$\in$ $B_{P}$ tali che esiste un albero SLD finitamente fallito con radice 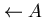$\leftarrow A$. Quindi se 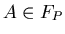$A \in F_{P}$ allora A non è conseguenza logica di P.

In generale si definisce la nozione di fallimento finito associato ad un programma logico nel modo seguente:

$FF_{0}(P) = \{ \}$

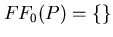
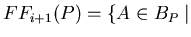$FF_{i+1}(P) = \{ A \in B_{P} \mid$ per ogni istanza ground 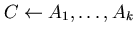$C \leftarrow A_{1}, \ldots, A_{k}$ di una clausola in P, o A e C unificano, o 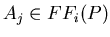$A_{j} \in FF_{i}(P)$ per qualche 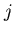$j$ in $[1,k] \}$

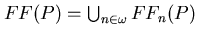$FF(P) = \bigcup_{n \in \omega} FF_{n}(P)$ è detto l'insieme di fallimento finito di P;

La regola di negazione come fallimento finito è così la seguente:

se 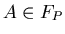$A \in F_{P}$ allora si inferisce $\neg A$.

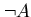Si può notare come la n.a.f., pur essendo più debole della CWA poiché vale che se 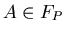$A \in F_{P}$ allora secondo CWA si deduce A, ma non il viceversa, è una regola effettiva e, dal momento che è facilmente implementabile in sistemi che fanno uso della risoluzione SLD, è la regola più frequentemente adottata per trattare la negazione.

Operazionalmente, però, non si può far ricorso ad una generica regola di computazione per decidere l'esistenza di un albero SLD finitamente fallito. Si possono verificare casi in cui l'albero di derivazione risulta infinito.

Per caratterizzare operazionalmente 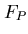$F_{P}$ si è quindi definito il concetto di risoluzione SLD fair. Una derivazione SLD è detta fair se è finita oppure è tale che, per ogni atomo B che vi compare, (una variante di) B viene prima o poi selezionata. Una regola di computazione R è fair se ogni derivazione SLD che usa R è fair. Un albero SLD è detto fair se ogni suo cammino corrisponde ad una derivazione fair.

Vale il seguente risultato che esprime la correttezza e la completezza della risoluzione SLD fair come implementazione della negazione come fallimento finito:

Teorema 3.1  

Dati un programma logico P ed un atomo 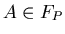$A \in F_{P}$, le seguenti affermazioni sono equivalenti:

• $A \in FF(P)$
• $A \not \in T_{P} \downarrow \omega$
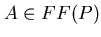
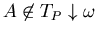
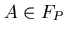• $A \in F_{P}$, ovvero esiste un albero SLD con radice 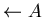$\leftarrow A$ finitamente fallito
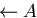• ogni albero SLD fair con radice $\leftarrow A$ è finitamente fallito

La completezza e la correttezza della regola di negazione come fallimento finito è stata dimostrata per una particolare teoria, il completamento di P comp(P) [Clark78], che intuitivamente rappresenta tutta la conoscenza espressa dal programma.

Dato un programma P, comp(P) si ottiene nel seguente modo:

ogni clausola di P del tipo

$$p(t) \leftarrow B_{1}, \ldots, B_{1}$$

viene trasformata in

$$p(x) \leftarrow E$$

dove E ha la seguente forma:

$$\exists y.(x=t \wedge B_{1} \wedge \ldots \wedge B_{k})$$

dove y sono le variabili originariamente presenti nella clausola, x sono variabili nuove e = è un nuovo simbolo di predicato. Quindi un predicato p è definito dall'insieme delle seguenti clausole

$$p(x) \leftarrow E_{1}$$

$\; \; \; \; \; \; \; \; \;\vdots$

$$p(x) \leftarrow E_{n}$$

Allora la definizione completata di p è

$$\forall x.(p(x) \leftrightarrow E_{1} \vee \ldots \vee E_{n})$$

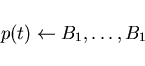
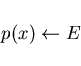
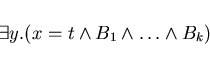
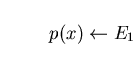
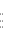
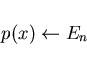
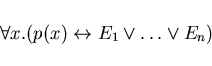
Se un predicato q di P non è definito nel programma, si assume che il completamento di q sia

$$\forall q(x) \leftrightarrow false$$

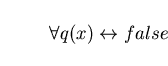
Denotiamo con 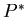$P^{*}$ l'insieme delle definizioni completate dei predicati di P.

È necessario disporre di una teoria che caratterizzi il predicato =; i seguenti assiomi definiscono la teoria dell'uguaglianza 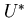$U^{*}$, che modella l'unificazione standard.

1. $\forall x.(x=x)$
2. $\forall x,y,z,w((x=y \wedge z=w) \rightarrow (x=z \wedge y=w))$
3. $\forall x,z ((x=z \leftrightarrow (f(x)=f(z))$
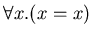
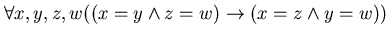
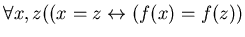
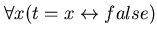4. $\forall x(t=x \leftrightarrow false)$, con t termine non variabile che non contiene x
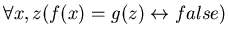5. $\forall x,z (f(x)=g(z) \leftrightarrow false)$, con f,g simboli di funzione del linguaggio e $f \neq g$.

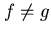Per indicare comp(P), è usata anche la notazione 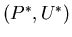$(P^{*},U^{*})$.

Il seguente risultato esprime il fatto che l'informazione positiva che può essere dedotta da comp(P) è esattamente la stessa deducibile da P.

Teorema 3.2 ( [Llo87])  

Sia P un programma logico, G un goal e 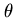$\theta$ una risposta per 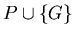$P \cup \{G \}$. Allora 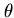$\theta$ è una risposta corretta per 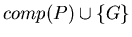$comp(P) \cup \{G \}$ se e solo se 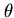$\theta$ è una risposta corretta per $P \cup \{G \}$.

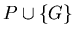La controparte procedurale alla definizione dichiarativa appena esposta è la risoluzione SLDNF, ottenuta estendendo la risoluzione SLD con la regola di negazione come fallimento finito.

La proprietà di correttezza di tale risoluzione è vincolata all'uso di una regola di calcolo con opportune caratteristiche, come evidenziato dal seguente esempio:

Esempio 3.1  

Consideriamo il programma generale P

$p \leftarrow \neg q(x)$

$q(a) \leftarrow$

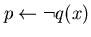
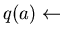
Se il letterale 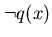$\neg q(x)$ può essere selezionato, si ottiene un albero SLDNF finitamente fallito per 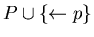$P \cup \{ \leftarrow p\}$, perché esiste una refutazione di 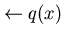$\leftarrow q(x)$ nella quale x è legato ad a. D'altra parte, 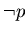$\neg p$ non è conseguenza logica di comp(P).

La regola di calcolo R necessaria è la seguente:

Definizione 3.1 (Regola di calcolo safe)  

• R seleziona solo sottogoal negativi ground
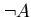• se $\neg A$ è il letterale negativo ground selezionato, R tenta di individuare una derivazione SLDNF finitamente fallita per A prima di continuare con il resto della computazione.

Quindi i sottogoal negativi possono esssere visti come lemmi che devono essere provati, per mezzo sempre della risoluzione SLDNF, prima di proseguire nel calcolo. Il fatto che possono essere selezionati solo sottogoal negativi ground implica che i legami delle variabili sono calcolati solo dalle chiamate con successo a sottogoal positivi. Perciò la negazione come fallimento è solo un test.

A Clark è dovuto il risultato di correttezza della risoluzione SLDNF rispetto al completamento di un programma:

Teorema 3.3  

Dati un programma generale P e un goal generale G, se 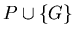$P \cup \{G \}$ ha un albero SLDNF finitamente fallito, allora G è una conseguenza logica di comp(P).

Per quanto riguarda la proprietà di completezza della risoluzione SLDNF, il seguente esempio mostra che non vale in generale:

Esempio 3.2  

Dato il programma logico P

$p(a) \leftarrow p(a)$

$q(b) \leftarrow$

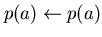
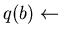
vale comp(P) 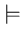$\models$ $\neg p(b)$. Ma il goal 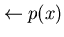$\leftarrow p(x)$ non ammette una refutazione SLDNF perché non esiste alcun albero SLD con radice 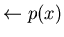$\leftarrow p(x)$ finitamente fallito.

Per ottenere la proprietà di completezza, si è dovuto ricorrere a restrizioni sintattiche sui goal e sulle clausole del programma. In questo modo si cerca di evitare il problema del floundering che consiste nell'ottenere durante una derivazione SLDNF un goal che contiene solo letterali negativi non ground, i quali non possono essere selezionati, per come è definita la regola di calcolo safe.

Poiché il verificarsi di tale problema è indecidibile nel caso di programmi logici, sono state individuate particolari condizioni che garantiscono l'assenza del floundering.

Un esempio è la nozione di allowedness [Llo87]:

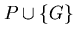$P \cup \{ G \}$ è allowed se ogni variabile di G appare in un letterale positivo di G e ogni variabile di una clausola di P compare nel corpo della clausola.

La prima condizione garantisce che tutti i letterali negativi di G sono ground non appena G non contiene letterali positivi, mentre la seconda garantisce che tutti i fatti del programma sono ground. Se vale che 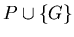$P \cup \{ G \}$ è allowed si dimostra che ogni derivazione di G non genera floundering e che ogni risposta calcolata è ground.